智力题
智力题一半都是都是在面试腾讯时候才会进行面试的问题,常见的问题就是包括烧绳子
烧绳子问题


题意:使用两个如何得到15分钟。
题解:可以进行对着烧,就是两边一起烧绳子,结果就是加速得到绳子,就是半小时了稍晚第一根绳子,然后第二根绳子还有半小时,接下来对第二根绳子接着对半烧,那就是只有15分钟了
最少试剂问题

这个是常见的的二进制编码问题,直接进行分组二进制按第一位是1的,第二位是1的
题意:使用最少的来进行检测那些人有病
题解:直接二进制检测,第一根试剂看有没有毒,第二根试剂看又没有毒,第三根有没有毒然后01二进制编码
或者直接使用二分法则,看那一边有问题,50,25,13,7,4,2,1
过桥问题
过桥问题
在漆黑的夜里,甲乙丙丁共四位旅行者来到了一座狭窄而且没有
护栏的桥边。如果不借助手电筒的话,大家是无论如何也不敢过
桥的。不幸的是,四个人一共只带了一只手电筒,而桥窄得只够
让两个人同时过。如果各自单独过桥的话,四人所需要的时间分
别是T1、T2、T3、T4分钟(假设T1<T2<T3<T4);而如
果两人同时过桥,所需要的时间就是走得比较慢的那个人单独行
动时所需的时间。
问题:如何设计一个方案,让这四人尽快过桥。
题意:就是一个桥只能通过两个人,一定要有light才可以进行通过,如何时间最短。
题解:1、使用最短作业的思路,就是每次都是最短的t1来送人过去,然后他自己回来
t2+t1+t3+t1+t4
2、还可以最后一次送走的t2,首先t1,t2一起来,然后t1回来,t3,t4一起走,t2回来,最后t1,t2一起走,那就是t2+t1+t4+t2+t2
接下来就是进行对比

推广:当推广到5个人,就是t1,t2出去,t1回来,那就变成4个人的情景


总结最终的差值就是:以此类推,
两种方案的差异,只与最快的人、次快的人和次慢的
人的单独过桥时间有关,而与其他人的
快慢无关。因此只需考虑最快的人时间+次慢的人的时间-2*次
块的人时间的大小即可选定实际方案。
赛马问题
问题:36匹马,6个赛道,至少赛多少次能挑出前3名(每次赛马成绩不变)
常见的多路归并排序方案
题解:使用正常的分组,每一个区间,可以得到6组,然后6次排序之后,每一个小组的排名都可以知道,可以知道每一组第一名,这样可以得到签6名,通过前三名所在的,再次进行比赛,可能第一个所在的小组前三都在他自己,第二个所在的组23在他自己,第三名所在的可能只有3,这样筛选出3,2,1个在1,2,3小组里面最后一轮进行比赛
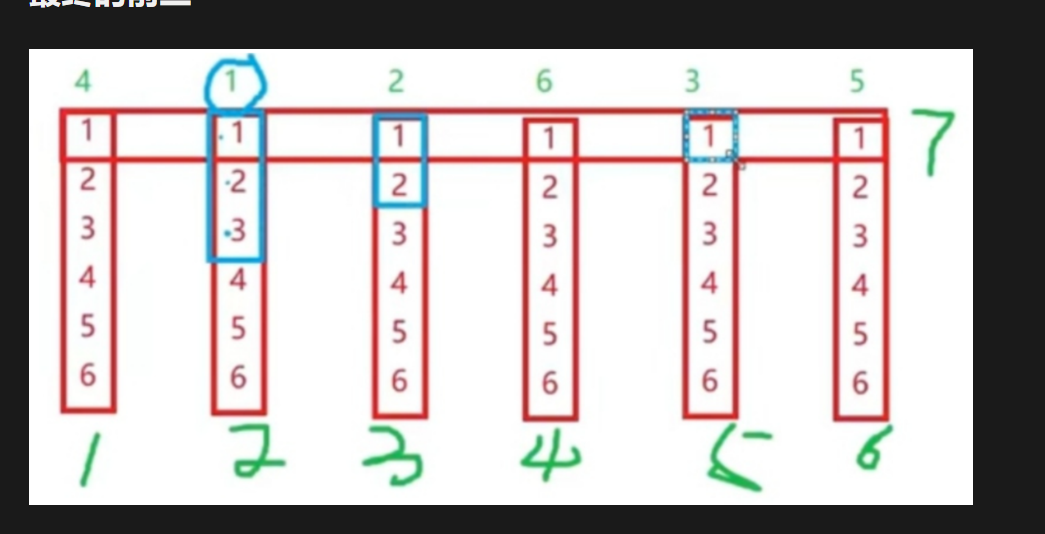
25匹马5条跑道找最快的5匹马,需要跑几次?
参考回答:最少8次最多9次
题解:参考上文的5组之后+1(得到第一)+1(得到23)
硬币问题
问题:有23枚硬币在桌上,10枚正面朝上。假设别人蒙住你
的眼睛,而你的手又摸不出硬币的反正面。让你用最好的方法
把这些硬币分成两堆,每堆正面朝上的硬币个数相同。(可以
进行硬币翻转)
题解:数学问题,假设一堆x个(y个正的,x-y反),另外一堆就是23-x(10-y个正的,13-x+y个反的),对第一堆x进行翻转,x-y=10-y,x=10,直接翻转10个
分盐问题
问题:有一个天平,2克和7克砝码各一个。如何利用天平砝码在三次内将140克盐分成50,90克两份。
2与7可以得到5(那就是可以得到左右相差10),或者9
题解:140-70-35开始做方程x+2=35-x+7,可以得到x=20,另外是15,35+15=50
先得到9-18
一共就是27la,剩下凑出23,等于4,那么就是凑方程
7+18-2=23
高楼扔鸡蛋问题

题解:传统的思路是通过二分法,来进行7次尝试,现在不行。只有两个,只能通过区间划分,传统10个一组,然后最大尝试机会(99楼,18次,如果是9楼,只要10次,这样就不平均),为了将19次方到10次里面,第一组x,第二组x-1,第三组x-2,一直加到1

为什么这样计算,1+x表示第一层楼的最后一个得到次数,2+x-1=x+1,表示第二次楼的最后一个的概率
8个球求质量轻
3,3,2,然后直接计算比较,3这个随机比较
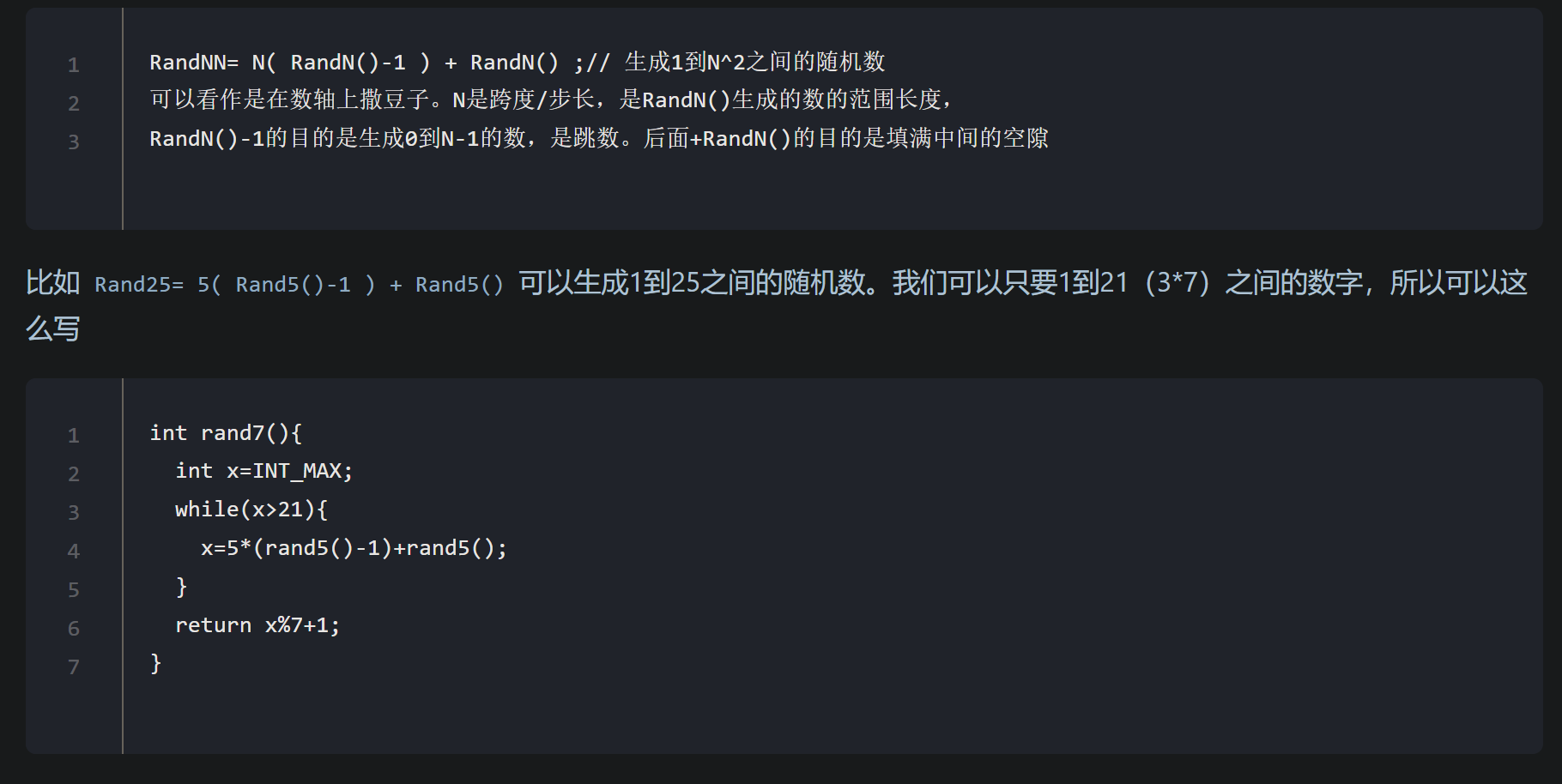
给定随机函数生成另外的随机函数

记住公式就行,表示生成的概率在1-21
- 首先生成平房以内的,一定是随机
- 然后再范围里找最近的
利用空瓶子换饮料

·第二种思维:利用借瓶子的思想
·。因为兑换一瓶饮料需要三个空瓶,这瓶饮料如果是找老板借来的,那么喝完后这个空瓶将会还给他,同时需要附赠给他
另外两个空瓶,即每消耗手里两个空瓶就获得一瓶饮料
。但是值得注意的是,上面只是一种假设,实际情况老板是不会借给你的,因此我们至少需要保留2个空瓶,这样可以在
998个瓶子剩下一个瓶子时,对其进行补足为3个空瓶,从而兑换一瓶新饮料
。此时使用998个瓶子进行上述的兑换,将获得499瓶饮料
。之前留下的两个瓶子正好无法兑换,最终获得饮料为1000+499=1499瓶
- 一般情况下2个瓶子就可以换回一个,因为-3+1,我只需要付出2个就行
- 最后我要保留最后两个,那就是1000-2=998,998/2=499
- 合计就是1000+499
三人三鬼问题

有三个人眼三个鬼要过河河上没挤只有条小船然后船一次只能渡一个人和一个鬼或者两个鬼或着两个人无论在那边岸上只有
是人比更少的情况下如两是一人三鬼两人,三鬼一人人会故鬼吃然而船又一定而要人或是操作才能抗行要有人或鬼划码)问,
如何安全的把三人三鬼渡过河对岸?

先两鬼过去。在一鬼回来。对面有一鬼。这边有三人两鬼。
再两鬼过去。在一鬼回来。对面有两鬼。这边有三人一鬼。
再两人过去。一人一鬼回来。对面一人一鬼。这边两人两鬼。
最后两人过去。一鬼回来。对面三人。这边三鬼。
剩下的就三个鬼二个过去一个回来在接另外个就ok了。
时分重合

在24小时里,时针走2圈,分针则走24圈。时针与分针重合大约22.22次,但考虑到仅提及时针与分针的重合,每次它们重合时
猜帽子的颜色
如果最后一个前面黑色帽子的数量是奇数就猜黑,不然就猜白色,剩下的就是数自己看到的黑色帽子的数量与上一轮给的是否一样(不一样就报白色)(白色是偶数)数量不一致就报黑,然后黑猫数量减一,与自己看到的黑猫进行比较,一致就是白,不一致就是黑。

一百个奴隶站成一纵列,每人头上随机戴上了黑色或白色的帽子。各人不知自己帽子的颜色,但却能看见自己前面所有人帽子的颜色。然后,从最后一个奴隶开始,每人只能用同一种声调和音量说一个字:“黑”或“白”。如果说中了自己帽子的颜色,就存活;说错了就被放出去处决。每个人的回答,所有奴隶都能听见,但是否说对,其他人不得而知。在这之前,所有奴隶可以聚在一起商量策略。问:如果所有奴隶都足够聪明且反应足够快,100个人的最大存活率是多少?
参考答案:这是一道经典的推理题。
最后一个人,如果看到前面有奇数顶黑帽子就说“黑”,否则说“白”。他有50%的生存机会。
其他人根据最后一个人的答案,记下黑帽的奇偶性。之后,每当再听到“黑”时,意味着已知的黑帽数量减一。
从倒数第二人开始,他依据自己看到的信息与前面传递的信息综合判断:若两者相同则报“白”,不同则报“黑”。
如此,除最后一人外的99最后一个黑色是代表技术个黑色帽子
然后自己看的数量与前面的数量奇偶性不一样,自己就是黑色的,之后黑色数量减一
然后进行记录的黑色与自己看到的黑色来比较


