数电小结

1.逻辑代数

第一章主要是讲逻辑代数，主要是离散数学的知识，这些知识在考验期间学过，就直接跳过。包括逻辑化简，最小项还有最大项。砌筑一个新的知识点就是卡洛图。下面简单介绍一下卡诺图。

卡诺图：用小方格来表示最小项，一个小方格代表一个最小项，然后将这些最小项按照相邻性排列起来（00 01 11 10）。

注意，是使用01还有11，不是01,10这样排列，这样是为了，能够2个都是1可以消除第一位，只留下一，还有10和00也是可以在一起进行消除的。

无关项：就是值未知的项，值为x，可0可1，一般是为了凑成最大的圈，就把x设置为1

卡诺图化简规则

基础知识：与或非异或，基本的门电路

电路分析，一般使用一下方法

编码器：就是把独热编码进行转化为相应的二进制代码把（0010）转化为二进制就是10（因为是2位使用，二进制就是10）

优先编码器：允许同时输入两个以上信号，并按优先级输出。例如：10-4线(如74LS147)、 8-3线(如74LS148)。就是输入多个有效信号，并且按照有限输出

译码器：3-8译码器，刚才把2进行编码输出为10，那么译码器就是把10，输出为0010

其中下面456是使能端，当45为低电平，6为高电平的时候才有效（因此，地址的开头可以设置在使能端，通过使能端的逻辑组合，来达到搜寻特定地址例如a8h到afh，后三位接到123，前面5位接到456，使用逻辑电路进行组合

74LS138应用1 实现逻辑函数：将逻辑函数转换成最小项表达式，再转换成与非—与非形式。用一片74138加与非门就可实现三变量逻辑函数。

例题：首先画出真值表，得到卡诺图，发现是y2y3y4y5，我们可以在最后面使用与非得到，前面就是选择2345的最小项

数据选择器：（4选一，需要2位来进行选择，因为2的2次方就是4，这两位数就是地址选择）

香浓化简法：把最终的逻辑函数，分成w还有-w，然后最下面进行设置数据选择器。

例题：2个8选一，构成16选一。

2片就是16选2，同时还需要设置，使能端，需要进行设置取反

rd的意识就是设置为0

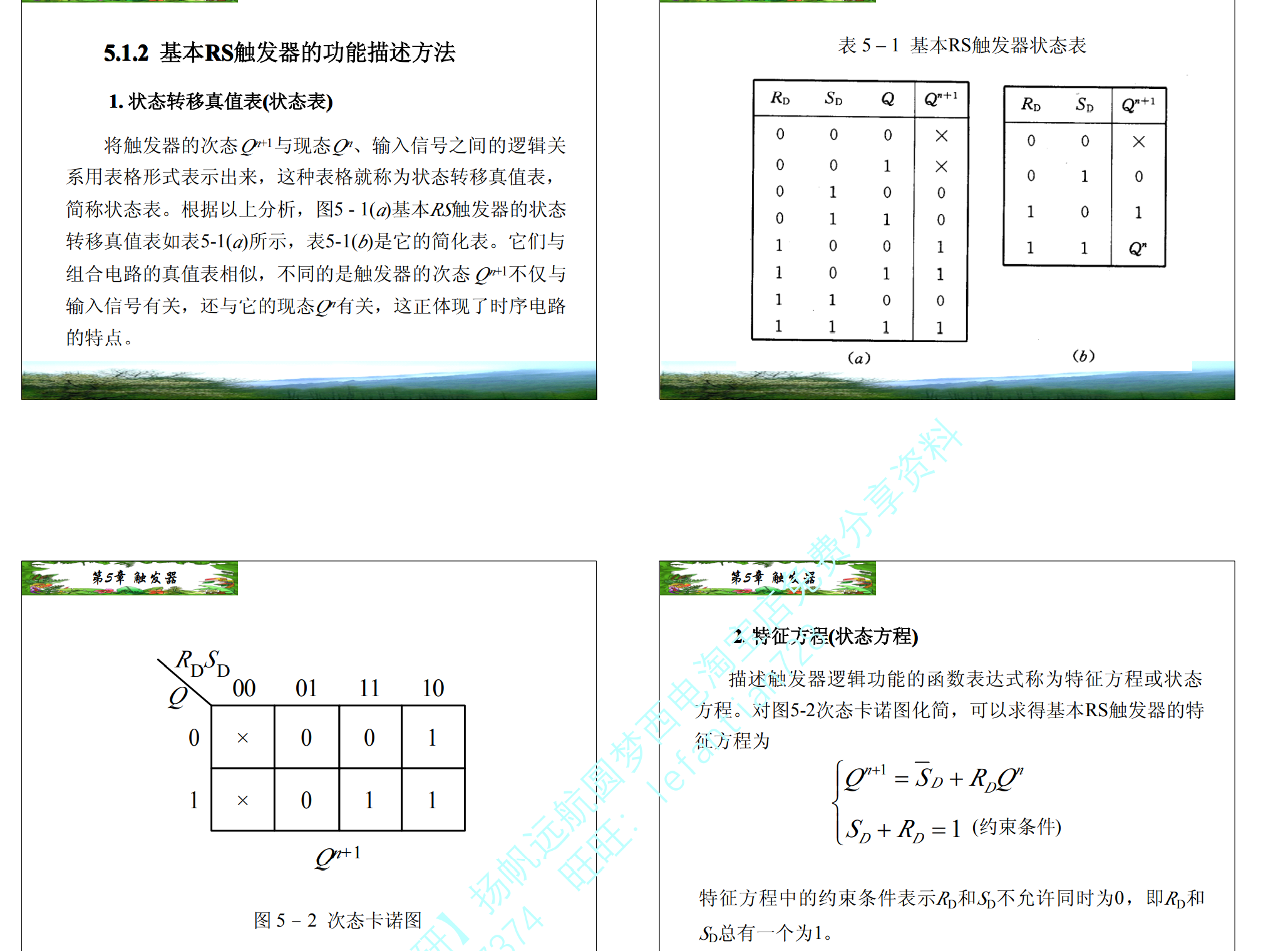
rs触发器：特点就是r=1，最后q的输出就是为0（r是resert的意思），当s=1，最后q就是1（s是set的意思），特征方程如下，rs

这个要换成或非门，只需要我们把r还有s设置真值表，，然后就可以得到逻辑函数，我们知道q非还有q是相反的，所以我们的约束条件是rs=0，但是当我们输入00的时候，这个条件就不成立，所以就是约束条件。

接下来就是d触发器（这个就是寄存器的原型，因为输入什么，输出什么）

下面就是t触发器

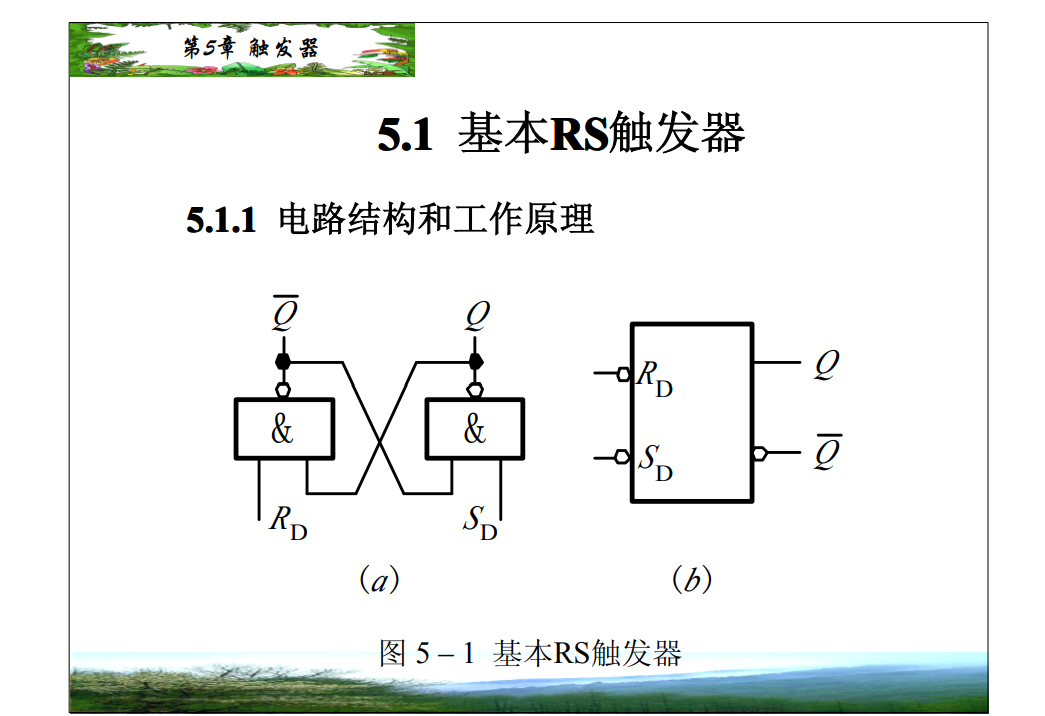
最后一个就是jk触发器，

他有上述的几个触发器的多个特点，j为1，设置0，k为设置为1，全0就是保持不变，全1就是进行取反

进行多个变形jk变d