4.数学知识

4.1质数

4.1.1基本算法

1
2
3
4
5
6
7
bool is_prime(int n){
if(i<2)return false;
for(int i=2;i<=n/;i++){
if(n%i==0)return false;
}
return true;
}

4.1.2分解质因数

从小到大尝试每一个因素

1
2
3
4
5
6
7
8
9
10
11
12
void divide(int n){
	for(int i=2;i<=n;i++){
		if(n%i==0){
		int s=0;
		#求出i的次数
		while(n%i==0){
		n/=s;
		i++;
		}
		}
	}
}

优化版本

n中至多质保函一个最多大于根号n的因子

1
2
3
4
5
6
7
8
9
10
11
12
13
14
void divide(int n){
	for(int i=2;i<=n/i;i++){
		if(n%i==0){
		int s=0;
		#求出i的次数
		while(n%i==0){
		n/=i;
		s++;
		}
		#这个循环是求出质数i的次数
		}
	}
	if(n>1)print(n)
}

4.1.3筛质数

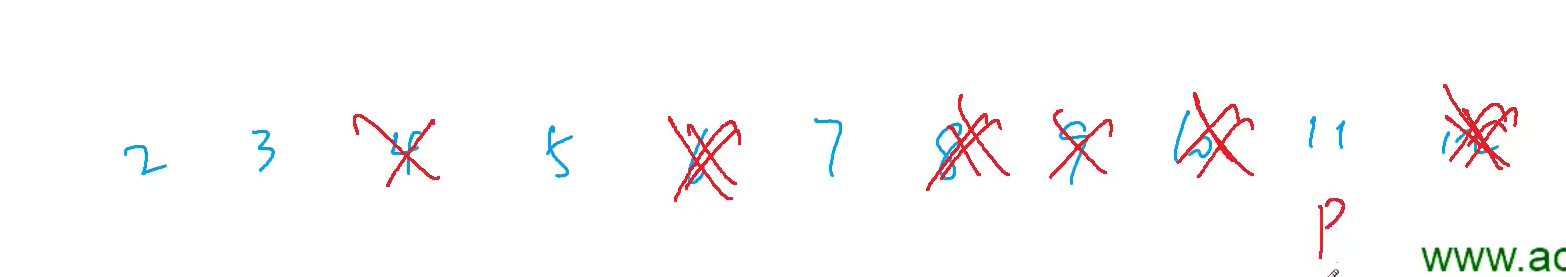
筛选倍数，直到n，是质数的倍数的直接pass

核心思想，反思倍数的，坑定不是质数

1
2
3
4
5
6
7
8
9
10
void get_prime(int n){
	for(int i=2;i<=n;i++){
		if(!st[i]){
		prime[cnt++]=i;
		}
		for(int j=i+i;j<=n;j+=i){
		st[i]=true;
		}
	}
}

下面这个是线性筛法

为什么是正确的，n只会倍最小质因子甩掉。从小到大枚举质数，每次筛掉i和质数

当break发生意味着prime【j】是i的最小质因子，因此primes【j】

第一次出现摸他为0 ，一定是质因子

如果摸不是0，pj也一定是pj*i的最小质因子