单纯形方法

使用

1.第一步：化标准形

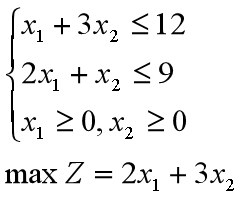
标准型的规定

1.目标函数要求max

2.约束条件均为等式

3.决策变量为非负约束

最终结果

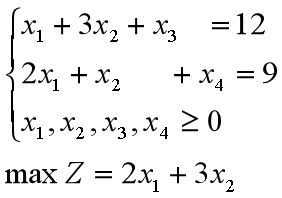
2.第二步：构建单纯形表

1.找出基向量，就是他们系数组成的矩阵是单位向量

2.把z函数的系数也加入这个矩阵，除了自己的系数是1，其余都为0，用行变换变成只有1个1，其余列上都为0

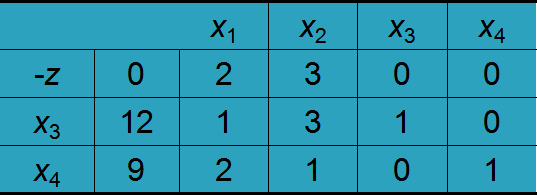
3.第三步：求解

1.找出θi里最大的所对应那一列

​ 如图，应该是3最大，对应的就是x2那一列，x2就是换入变量，再求b/aij,就是b那一列除x2对应的那一列，那个最小就是，那个元素的行向量对应的向量换出变量（b>0才可以除，若都小于等于0，则无解）12/3=4,9/1=9,4小，x3就是换出变量

2.把x2那一列化成010，保证只有x2与x3相交的为1，其他的都为0，在x2列

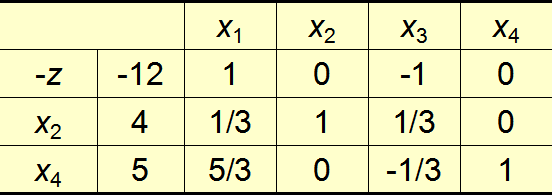
3.重复1,2两步，直到z的系数都小于等于0

此时x1是换入，x4是换出，变成001

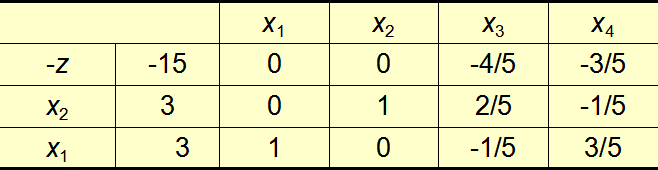
4.结束

当θi都小于等于0是结束，x*=（3,3,0,0）T，z=15

5.总结

解的分类

1.唯一最优解

当所有非基变量的检验数都小于零，则原问题有唯一最优解

2.无穷多个最优解

当所有非基变量的检验数都小于等于零，注意有等于零的检验数，则有无穷多个最优解，有0

非基向量就可以随便加也无影响，所以是无穷个

3.无界解

当任意一个大于零的非基变量的检验数，其对应的ajk（求最小比值的分母）都小于等于零时，则原问题有无界解

就是b/aij<=0,无法找到换出的变量

4.无可行解

添加人工变量后的问题，当所有非基变量的检验数都小于等于零，而基变量中有人工变量时，则原问题无可行解